Pricing under RI w/o Endogenous Feedback

This document goes through a couple of examples for solving pricing under rational inattention without endogenous feedback using the DRIPs package.

to run and modify the following code (no software is needed on the local machine).

See Afrouzi and Yang (2020) for background on the theory.

Ex. 1A: One Shock Case
Ex. 1B: Two Shocks Case

Ex. 1A: One Shock Case

There is a measure of firms indexed by $i\in[0,1]$. Firm $i$ chooses its price $p_{i,t}$ at time $t$ to track its ideal price $p_{i,t}^*$. Formally, her flow profit is $-(p_{i,t}-p_{i,t}^*)^2$

We start by assuming that $p_{i,t}^*=q_t$ where

\[\begin{aligned} \Delta q_t&=\rho \Delta q_{t-1}+u_t,\quad u_t\sim \mathcal{N}(0,\sigma_u^2) \end{aligned}\]

Here $q_t$ can be interpreted as money growth or the nominal aggregate demand. Therefore, the state-space representation of the problem is

\[\begin{aligned} \vec{x}_{t}&=\left[\begin{array}{c} q_{t}\\ \Delta q_{t} \end{array}\right] = \underset{\mathbf{A}}{\underbrace{\left[\begin{array}{cc} 1 & \rho \\ 0 & \rho \\ \end{array}\right]}}\, \vec{x}_{t-1} + \underset{\mathbf{Q}}{\underbrace{\left[\begin{array}{c} \sigma_u \\ \sigma_u \\ \end{array}\right]}}\, u_t, \\ p_{i,t}^*&=\underset{\mathbf{H}}{\underbrace{\left[\begin{array}{c} 1 \\ 0 \\ \end{array}\right]}}'\vec{x}_t \end{aligned}\]

Initialization

Include the package:

using DRIPs;
nothing #hide

Assign value to deep parameters and define the structure of the problem

ρ   = 0.6;        #persistence of money growth
σ_u = 1;          #std. deviation of shocks to money growth
nothing #hide

Primitives of the DRIP:

ω   = 100;
β   = 0.96^0.25;
A   = [1 ρ; 0 ρ];
Q   = σ_u*[1; 1];
H   = [1; 0];
nothing #hide

Solution

ex1 = Drip(ω,β,A,Q,H);
nothing #hide

Measure Performance

using BenchmarkTools;
@benchmark Drip(ω,β,A,Q,H) setup = (ω = 100*rand()) # solves and times the function for a random set of ω's

BenchmarkTools.Trial: 
  memory estimate:  45.36 KiB
  allocs estimate:  446
  --------------
  minimum time:     28.484 μs (0.00% GC)
  median time:      100.153 μs (0.00% GC)
  mean time:        113.236 μs (13.17% GC)
  maximum time:     3.653 ms (95.32% GC)
  --------------
  samples:          10000
  evals/sample:     1

IRFs

ex1irfs = irfs(ex1, T = 20);
nothing #hide

Let's plot how the average price $p=\int_0^1 p_{i,t}di$ responds to a shock to money growth:

using Plots, LaTeXStrings; pyplot();
plot(1:ex1irfs.T,[ex1irfs.x[1,1,:],ex1irfs.a[1,1,:]],
    xlabel     = "Time",
    label      = [L"Nominal Agg. Demand ($q$)" L"Price ($p$)"],
    title      = "IRFs to 1 Std. Dev. Expansionary Shock",
    xlim       = (1,ex1irfs.T),
    lw         = 3,
    legend     = :bottomright,
    legendfont = font(12),
    tickfont   = font(12),
    framestyle = :box)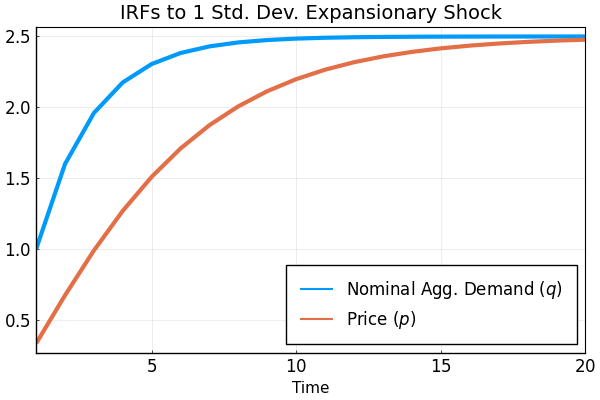

We can also plot the IRFs of inflation $\pi_t\equiv p_t-p_{t-1}$ and output $y_t\equiv q_t-p_t$ to 1 percent expansionary shock to $q$:

p1 = plot(1:ex1irfs.T,ex1irfs.x[1,1,:]-ex1irfs.a[1,1,:],
    title  = L"Output ($y_t$)")

p2 = plot(1:ex1irfs.T,[ex1irfs.a[1,1,1];ex1irfs.a[1,1,2:end]-ex1irfs.a[1,1,1:end-1]],
    title  = L"Inflation ($\pi_t$)")

plot(p1,p2,
    layout     = (1,2),
    xlim       = (1,ex1irfs.T),
    lw         = 3,
    legend     = false,
    tickfont   = font(12),
    framestyle = :box)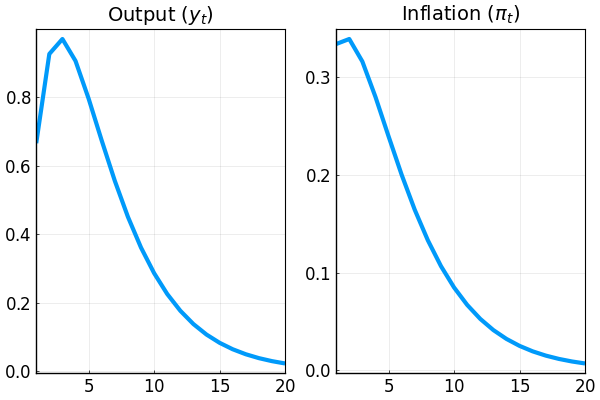

Ex. 1B: Two Shocks Case

Suppose now that $p_{i,t}^*=q_t-z_{t}$ where

\[\begin{aligned} \Delta q_t&=\rho \Delta q_{t-1}+u_t,\quad u_t\sim \mathcal{N}(0,\sigma_u^2) \\ z_{t}&\sim \mathcal{N}(0,\sigma_z^2) \end{aligned}\]

Here $q_t$ can be interpreted as money growth and $z_{i,t}$ as an idiosyncratic TFP shock. Therefore,

\[\begin{aligned} \vec{x}_{t}&=\left[\begin{array}{c} q_{t}\\ \Delta q_{t} \\ z_{t} \end{array}\right] = \underset{\mathbf{A}}{\underbrace{\left[\begin{array}{ccc} 1 & \rho & 0\\ 0 & \rho & 0\\ 0 & 0 & 0 \\ \end{array}\right]}}\, \vec{x}_{t-1} + \underset{\mathbf{Q}}{\underbrace{\left[\begin{array}{cc} \sigma_u & 0 \\ \sigma_u & 0 \\ 0 & \sigma_z \\ \end{array}\right]}}\, \left[\begin{array}{c} u_t \\ z_{t} \\ \end{array}\right], \\ p_{i,t}^*&=\underset{\mathbf{H}}{\underbrace{\left[\begin{array}{c} 1 \\ 0 \\ -1 \\ \end{array}\right]}}'\vec{x}_{t} \end{aligned}\]

Initialization

Assign values:

ρ   = 0.6;        #persistence of money growth
σ_u = 1;          #std. deviation of shocks to money growth
σ_z = √10;      #std. deviation of idiosyncratic shock
nothing #hide

Specifying the primitives of the drip

ω   = 100;
β   = 0.96^0.25;
A   = [1 ρ 0; 0 ρ 0; 0 0 0];
Q   = [σ_u 0; σ_u 0; 0 σ_z];
H   = [1; 0; -1];
nothing #hide

Solution

ex2  = Drip(ω,β,A,Q,H);
nothing #hide

Measure Performance

@benchmark Drip(ω,β,A,Q,H) setup = (ω = 100*rand()) # solves and times the function for a random set of ω's

BenchmarkTools.Trial: 
  memory estimate:  110.42 KiB
  allocs estimate:  784
  --------------
  minimum time:     104.317 μs (0.00% GC)
  median time:      241.705 μs (0.00% GC)
  mean time:        252.607 μs (6.60% GC)
  maximum time:     3.835 ms (90.94% GC)
  --------------
  samples:          10000
  evals/sample:     1

IRFs

ex2irfs = irfs(ex2, T = 20);
nothing #hide

To get the IRFs simply use the law of motion for actions:

p1 = plot(1:ex2irfs.T,[ex2irfs.x[1,1,:],ex2irfs.a[1,1,:]],
    title  = L"IRFs to $q$ shock");
p2 = plot(1:ex1irfs.T,[ex2irfs.x[1,2,:],ex2irfs.a[1,2,:]],
    title  = L"IRFs to $z$ shock");

plot(p1,p2, layout = (1,2),
    xlabel     = "Time",
    label      = [L"Agg. Demand ($q$)" L"Price ($p$)"],
    xlim       = (1,ex2irfs.T),
    lw         = 3,
    legend     = :bottomright,
    legendfont = font(12),
    tickfont   = font(12),
    framestyle = :box)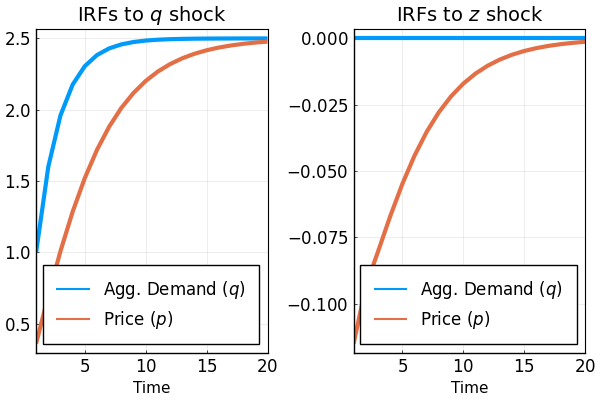

More IRFs:

p1 = plot(1:ex2irfs.T,ex2irfs.x[1,1,:]-ex2irfs.a[1,1,:],
    title  = L"Output ($q_0\to y_t$)");

p2 = plot(1:ex2irfs.T,[ex2irfs.a[1,1,1];ex2irfs.a[1,1,2:end]-ex2irfs.a[1,1,1:end-1]],
    title  = L"Inflation ($q_0\to \pi_t$)")

p3 = plot(1:ex2irfs.T,ex2irfs.x[1,2,:]-ex2irfs.a[1,2,:],
    title  = L"Output ($z_0\to y_t$)");

p4 = plot(1:ex2irfs.T,[ex2irfs.a[1,2,1];ex2irfs.a[1,2,2:end]-ex2irfs.a[1,2,1:end-1]],
    title  = L"Inflation ($z_0\to \pi_t$)")

plot(p1,p2,p3,p4, layout = (2,2),
    xlim       = (1,ex2irfs.T),
    lw         = 3,
    legend     = false,
    tickfont   = font(12),
    framestyle = :box)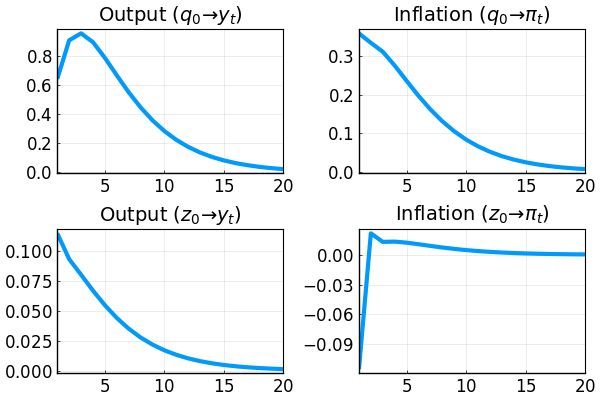

This page was generated using Literate.jl.